Klein Prep

Due Date: August 18, 2023
Hello Klein Prep Students,

------------------------------------------------------

My Period 3 KP students complete this:

P3 - KP Computer Science: Multiple courses
Click on the link on the next line and sign up.
https://www.khanacademy.org/join/W895GZPS
Klein Prep Period 4 students,

-------------------------------------------------------

My Period 4 KP students complete this:

P4 - KP Computer Science Assignment.
Click on the link on the next line and sign up.
https://www.khanacademy.org/join/THU348DM

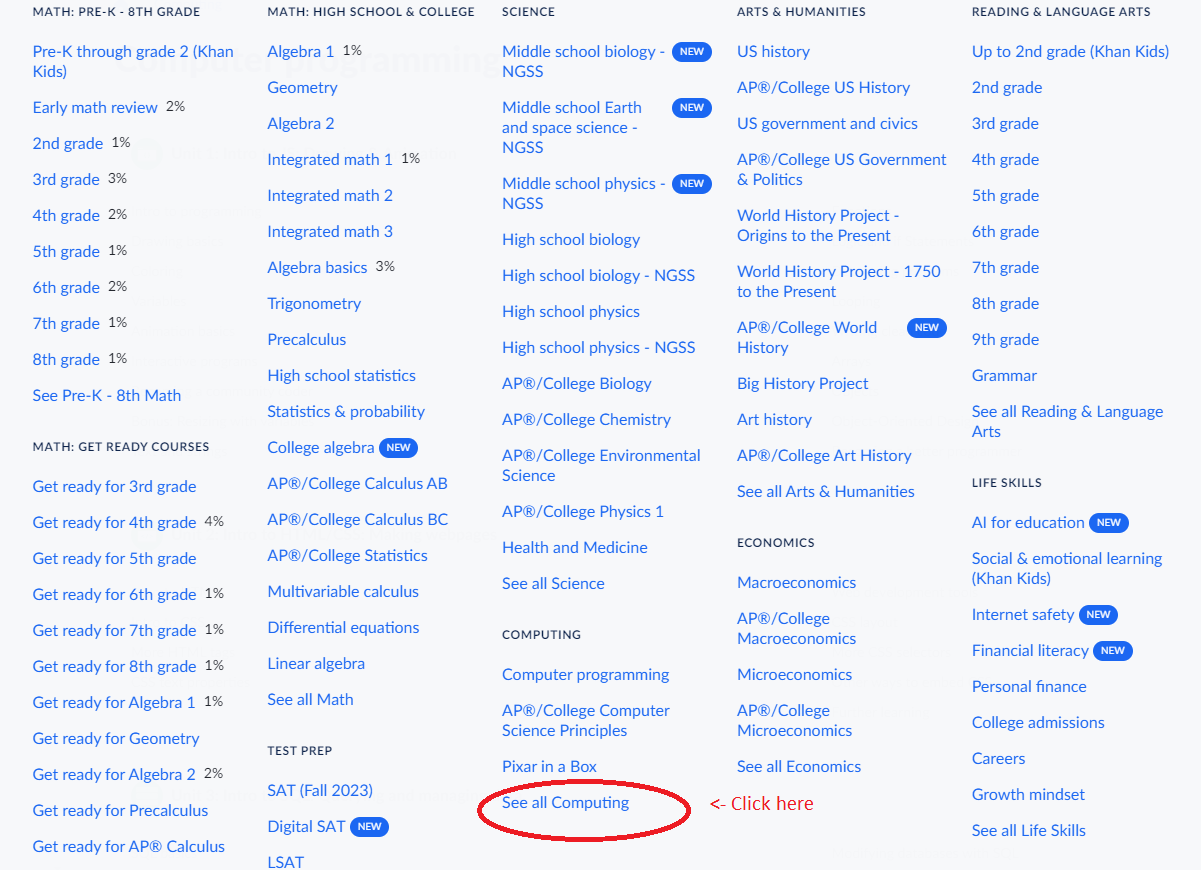
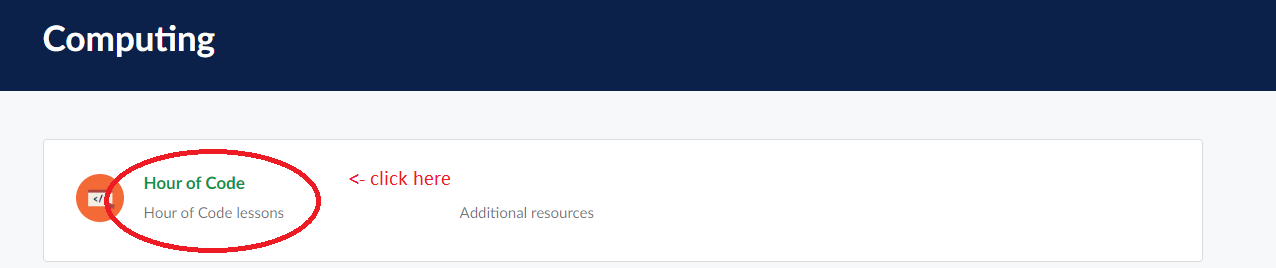
Due Date: August 25, 2023
Count in binary - PX_lastname_count_Binary

Count in Binary on either the Board or
on Paper per Mr. Cusack instructions.
Take a picture with your name and class period on it.
Your file name will be PX_lastname_count_Binary.jpg
Turn it into google classroom.

Read the following notes about 
counting binary and converting bases.

Counting in binary is a way of representing
numbers using only two digits: 0 and 1.
It's the foundation of how computers store 
and process information, as they use binary digits (bits)
to represent data. Here's how you can count in binary:

Binary Digits (Bits): In binary, each digit is called 
a "bit." A bit can have two possible values: 0 or 1. 
It's the equivalent of a decimal digit (0-9) in 
the decimal number system.

Binary Place Value System: Similar to the decimal 
system, binary uses a place value system. 
Each position from right to left represents a 
power of 2. The rightmost position 
represents 2^0 (which is 1), 
the next position to the left represents 2^1 
(which is 2), then 2^2 (which is 4), and so on.

Counting Procedure:

Start with the rightmost position, which 
represents 2^0, and put a 0 there.
Move to the next position to the left 
(representing 2^1), and put a 1 there.
Continue this pattern, alternating between
0 and 1 for each position to the left.
When you reach the highest position you 
want to count up to, reset all the 
digits to the right to 0 and increase 
the leftmost digit by 1.
Let's walk through counting from 0 
to 15 in binary:

Decimal	Binary
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111
As you can see, each time you count 
up by one, you increment the rightmost
bit, and when that bit reaches 2, it
becomes 0 again, and you carry over 
to the next bit to the left. This is
very similar to how counting works
in the decimal system, but with only 
two possible values for each digit.
---------------------------
Converting a number from base 10 
(decimal) to another base involves 
dividing the decimal number repeatedly
by the desired base and noting the 
remainders at each step. The remainders 
will form the digits of the new 
representation in the target base.

Due Date: August 23, 2023
Count in Octal - PX_lastname_count_Octal

Count in Octal on either the Board or
on Paper per Mr. Cusack instructions.
Take a picture with your name and class period on it.
Your file name will be PX_lastname_count_Octal.jpg
Turn it into google classroom.

Read the notes below:
Counting in octal involves using a 
base-8 numbering system, which means
that each digit can have one of eight 
possible values: 0, 1, 2, 3, 4, 5, 6, 
and 7. Octal is less common than 
binary and hexadecimal (base-16),
but it's still used in some contexts.
Here's how to count in octal:

1. **Octal Digits:**
   - Octal uses the digits 0 through 7.
   These digits represent different values
   just like the digits in the decimal system (0-9).

2. **Octal Place Value System:**
   - Similar to binary and decimal, 
   octal employs a place value system.
   - Each position from right to left 
   represents a power of 8. The 
   rightmost position represents 8^0 
   (which is 1), the next position to
   the left represents 8^1 (which is 8), 
   then 8^2 (which is 64), and so on.

3. **Counting Procedure:**
   - Start with the rightmost position (8^0), 
   and put a digit between 0 and 7.
   - Move to the left, increasing the power
   of 8 by 1 each time, and again, place a
   digit between 0 and 7.
   - Continue this pattern as you count up.

Let's count from 0 to 15 in octal:

| Decimal | Octal |
|---------|-------|
| 0       | 0     |
| 1       | 1     |
| 2       | 2     |
| 3       | 3     |
| 4       | 4     |
| 5       | 5     |
| 6       | 6     |
| 7       | 7     |
| 8       | 10    |
| 9       | 11    |
| 10      | 12    |
| 11      | 13    |
| 12      | 14    |
| 13      | 15    |
| 14      | 16    |
| 15      | 17    |

Notice that when the digit in a position
reaches 7, it becomes 0 again, and you 
carry over to the next position to the 
left, just like in other place value
systems. Counting in octal is a way 
to represent numbers using a base-8 
system, which can be useful in some 
computing and mathematical contexts.

Due Date: August 23, 2023
Count in Hexadecimal - PX_lastname_count_Hex

Count in Hexadecimal on either the Board or
on Paper per Mr. Cusack instructions.
Take a picture with your name and class period on it.
Your file name will be PX_lastname_count_Hex.jpg
Turn it into google classroom.

Counting in hexadecimal involves 
using a base-16 numbering system, 
which means that each digit can 
have one of sixteen possible 
values: 0, 1, 2, 3, 4, 5, 6, 7,
8, 9, A, B, C, D, E, and F. Hexadecimal
is commonly used in computer science
and programming as a more compact
way to represent binary data. 
Here's how to count in hexadecimal:

1. **Hexadecimal Digits:**
   - Hexadecimal uses the digits 
   0 through 9 for values 0 to 9, 
   and letters A through F for 
   values 10 to 15.
   - A corresponds to 10, B to 
   11, C to 12, D to 13, E to 14, 
   and F to 15.

2. **Hexadecimal Place Value System:**
   - Similar to other numbering 
   systems, hexadecimal employs
   a place value system.
   - Each position from right to
   left represents a power of 16.
   The rightmost position represents
   16^0 (which is 1), the next 
   position to the left represents
   16^1 (which is 16), then 16^2 
   (which is 256), and so on.

3. **Counting Procedure:**
   - Start with the rightmost
   position (16^0), and put a 
   digit between 0 and F.
   - Move to the left, increasing
   the power of 16 by 1 each time, 
   and again, place a digit between 0 and F.
   - Continue this pattern as you count up.

Let's count from 0 to 15 in hexadecimal:

| Decimal | Hexadecimal |
|---------|-------------|
| 0       | 0           |
| 1       | 1           |
| 2       | 2           |
| 3       | 3           |
| 4       | 4           |
| 5       | 5           |
| 6       | 6           |
| 7       | 7           |
| 8       | 8           |
| 9       | 9           |
| 10      | A           |
| 11      | B           |
| 12      | C           |
| 13      | D           |
| 14      | E           |
| 15      | F           |

When a digit reaches F, it becomes 
0 again, and you carry over to the
next position to the left, similar
to other place value systems. 
Counting in hexadecimal provides
a convenient way to represent 
binary data, as each hexadecimal
digit corresponds to exactly four 
binary digits (bits), making it 
easier to work with and visualize
in programming and computer-related tasks.
Converting a number from base 
10 (decimal) to base 16 (hexadecimal)
involves dividing the decimal
number repeatedly by 16 and 
noting the remainders at each 
step. The remainders will form 
the hexadecimal digits of the 
new representation. Here's a 
step-by-step process for converting 
from decimal to hexadecimal:

1. **Divide and Record Remainders:**
   - Divide the decimal number  by 16.
   - Note the remainder from the division.
   This remainder will be one of the 
   hexadecimal digits (0-9 or A-F).
   - The quotient obtained from the 
   division becomes the new value of 

2. **Repeat Division:**
   - Repeat the division and remainder
   process using the new value of  
   obtained from the previous step.
   - Continue this process until the
   quotient becomes 0.

3. **Digits in Reverse Order:**
   - Write down the remainders obtained 
   from each division in reverse order.
   These remainders will form the 
   hexadecimal representation.

Due Date: August 25, 2023

java primitive data types "byte" size - PX_lastname_byte.png

-You will list all 8 of the java primitive data types
     -indicate which are a part of the APCS A subset.
-Explain why 127 is the largest number
	-allowed in the java data type "byte".
	-Also, explain why I am able to store -128
	-into the java data type "byte".

Take a picture of your work of the board showing your work.
Your file name will be PX_Lastname_byte.png
Turn it into google classroom.

Read the notes below:

Java eight primitive data types are:
byte 8 bits
short 16 bits
int 32 bits
long 64 bits
float  1/2 the size of double (decimal format)
double 2 times the size of float (decimal format)
boolean true/false
char single character


Why is java data type byte only stores up to 127 positive and 128 negative.
In Java, the `byte` type is an 8-bit data type that can store integer values in the range of -128 to 127. The reason for this range is due to the way binary representation and two's complement arithmetic work.

In two's complement representation, which is commonly used to represent signed integers in computers, the most significant bit (MSB), which is the leftmost bit, is used as the sign bit. If the sign bit is 0, the number is positive, and if it's 1, the number is negative. The remaining bits represent the magnitude of the number.

For an 8-bit two's complement representation, the range of values is from -2^7 (-128) to 2^7 - 1 (127). This is because the MSB represents the sign, and the remaining 7 bits represent the magnitude of the number.

Here's how it works:

- Binary representation of -128: 10000000
- Binary representation of -1: 11111111
- Binary representation of 0: 00000000
- Binary representation of 127: 01111111

As you can see, the leftmost bit (MSB) in these binary representations determines the sign of the number. If it's 0, the number is positive, and if it's 1, the number is negative. The `byte` type in Java follows this two's complement representation, allowing it to represent integers in the range of -128 to 127. This range is often sufficient for many use cases involving small integers, while also optimizing memory usage by using only 8 bits per value.

Due Date: August 25, 2023
Ascii Table - PX_lastname_Ascii.mp4

Complete Ascii table encoding on  per Mr. Cusack instructions.
Be sure to put your name and class period on the board.
You will be recording your demo modeled after Mr. Cusack demonstration.
Your file name will be PX_lastname_Ascii.mp4
Drop this off into google classroom.

Read the notes below:

Gain an understanding of Ascii Table and how it relates to the Unicode table.
The ASCII (American Standard Code for Information Interchange) table is a character encoding standard that assigns unique numeric codes to represent characters in computers and communication equipment. It was developed in the early days of computing to provide a standardized way to represent characters using binary numbers, making it possible for different computer systems to communicate and exchange text-based information.

The ASCII table consists of a total of 128 character codes, each assigned a unique 7-bit binary number, ranging from 0 to 127. These codes represent a variety of characters, including letters (both uppercase and lowercase), digits, punctuation marks, control characters (such as newline and tab), and special characters.

For example, some common ASCII codes and their corresponding characters are:

- ASCII Code 65: Represents the uppercase letter 'A'
- ASCII Code 97: Represents the lowercase letter 'a'
- ASCII Code 48: Represents the digit '0'
- ASCII Code 32: Represents the space character
- ASCII Code 10: Represents the newline character

The ASCII table provided a consistent way to represent characters across different computer systems, making it possible to share text-based data and messages between different devices and software. However, as computing evolved and more characters were needed to represent different languages, symbols, and characters, the limitations of the 7-bit ASCII encoding became apparent.

To accommodate a wider range of characters, different character encoding standards like ISO-8859 and eventually Unicode were developed. Unicode, in particular, aims to cover virtually all characters and symbols from all writing systems, and it provides multiple encoding schemes, including UTF-8 and UTF-16, which can represent characters using more than 8 bits as needed.

While ASCII itself has largely been surpassed by more comprehensive and flexible character encodings like Unicode, its legacy remains in the foundation of many programming languages and systems, and it still serves as the basis for the first 128 characters of Unicode.

Due Date: August 25, 2023
Calculate subtraction in Binary - PX _lastname_2Complement.mp4

Complete a demo of subtraction on the board per Mr. Cusack instructions.
Be sure to put your name and class period on the board.
You will be recording your demo modeled after Mr. Cusack demonstration.
Your file name will be PX_lastname_2Complement.mp4
Drop this off into google classroom.

Read the notes below:

Calculate subtraction in Binary either the Board or
on Paper per Mr. Cusack instructions.
Take a picture with your name and class period on it.
Your file name will be PX _lastname_2Complement.jpg
Turn it into google classroom.

Read the notes below:

In Java, the two's complement is a fundamental concept used for representing and manipulating signed integer values. Two's complement is a binary representation that allows negative numbers to be represented by flipping the bits of the positive counterpart and then adding 1. This representation simplifies arithmetic operations and provides a convenient way to handle both positive and negative integers within a fixed number of bits.

Here's how two's complement works in Java:
1. **Positive Numbers:**
   - Positive integers are represented using their regular binary representation, with no modifications needed. For example, the decimal number 5 would be represented as `00000101` in binary using 8 bits.

2. **Negative Numbers:**
   - To represent a negative number, you first take the two's complement of its positive counterpart.
   - To find the two's complement, you invert (flip) all the bits (0s become 1s and 1s become 0s) of the positive binary representation.
   - Then, add 1 to the inverted result.

For example, let's consider an 8-bit representation:

- Decimal -3: Its positive counterpart is 3, which is `00000011` in binary.
- Invert the bits: `11111100`
- Add 1: `11111101`

So, the two's complement representation of -3 in an 8-bit system is `11111101`.

When you perform arithmetic operations in Java, including addition, subtraction, multiplication, and division, the two's complement representation ensures that these operations work consistently for both positive and negative numbers. The use of two's complement simplifies the hardware design of processors and allows them to perform arithmetic operations using the same logic gates for both signed and unsigned integers.

In modern computing systems, the details of two's complement representation are handled by the hardware and the programming language, like Java, abstracts these complexities away from the programmer. You can work with positive and negative integers in a natural way, and the underlying two's complement representation takes care of the required conversions and arithmetic operations.