AP Computer Science Principles
*********
*********
Due Date: August 21, 2023
Hello my AP Principles Students,
---------------------------------------------------------
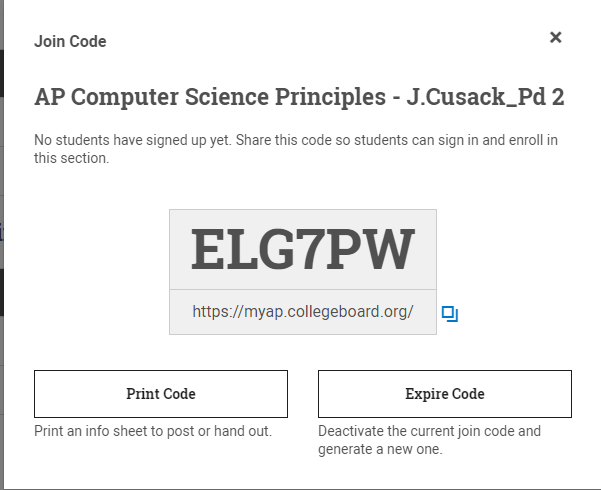
Period 2 - AP Principles Students,
Please join my Class.
Click on my link on the next line.
https://www.khanacademy.org/join/B66JM2HK
Your assignment is below:
Complete Digital information.
It has been assigned to you.
---------------------------------------------------------
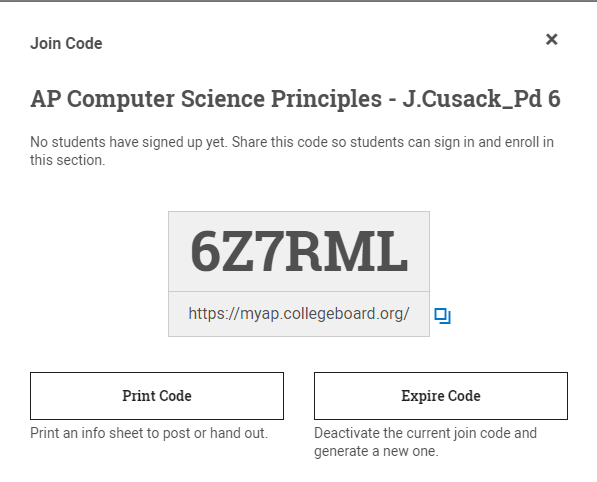
Period 6 - AP Principles Students,
Please join my Class.
Click on my link on the next line.
https://www.khanacademy.org/join/29RYGV3T
Your assignment is below:
Complete Digital information.
It has been assigned to you.
*********
*********
Due Date: August 25, 2023
*********
*********
Due Date: August 25, 2023
Count in binary - PX_lastname_count_Binary
Count in Binary on either the Board or
on Paper per Mr. Cusack instructions.
Take a picture with your name and class period on it.
Your file name will be PX_lastname_count_Binary.jpg
Turn it into google classroom.
Read the following notes about
counting binary and converting bases.
Counting in binary is a way of representing
numbers using only two digits: 0 and 1.
It's the foundation of how computers store
and process information, as they use binary digits (bits)
to represent data. Here's how you can count in binary:
Binary Digits (Bits): In binary, each digit is called
a "bit." A bit can have two possible values: 0 or 1.
It's the equivalent of a decimal digit (0-9) in
the decimal number system.
Binary Place Value System: Similar to the decimal
system, binary uses a place value system.
Each position from right to left represents a
power of 2. The rightmost position
represents 2^0 (which is 1),
the next position to the left represents 2^1
(which is 2), then 2^2 (which is 4), and so on.
Counting Procedure:
Start with the rightmost position, which
represents 2^0, and put a 0 there.
Move to the next position to the left
(representing 2^1), and put a 1 there.
Continue this pattern, alternating between
0 and 1 for each position to the left.
When you reach the highest position you
want to count up to, reset all the
digits to the right to 0 and increase
the leftmost digit by 1.
Let's walk through counting from 0
to 15 in binary:
Decimal Binary
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
10 1010
11 1011
12 1100
13 1101
14 1110
15 1111
As you can see, each time you count
up by one, you increment the rightmost
bit, and when that bit reaches 2, it
becomes 0 again, and you carry over
to the next bit to the left. This is
very similar to how counting works
in the decimal system, but with only
two possible values for each digit.
---------------------------
Converting a number from base 10
(decimal) to another base involves
dividing the decimal number repeatedly
by the desired base and noting the
remainders at each step. The remainders
will form the digits of the new
representation in the target base.
*********
*********
Due Date: August 25, 2023
Count in Octal - PX_lastname_count_Octal
Count in Octal on either the Board or
on Paper per Mr. Cusack instructions.
Take a picture with your name and class period on it.
Your file name will be PX_lastname_count_Octal.jpg
Turn it into google classroom.
Read the notes below:
Counting in octal involves using a
base-8 numbering system, which means
that each digit can have one of eight
possible values: 0, 1, 2, 3, 4, 5, 6,
and 7. Octal is less common than
binary and hexadecimal (base-16),
but it's still used in some contexts.
Here's how to count in octal:
1. **Octal Digits:**
- Octal uses the digits 0 through 7.
These digits represent different values
just like the digits in the decimal system (0-9).
2. **Octal Place Value System:**
- Similar to binary and decimal,
octal employs a place value system.
- Each position from right to left
represents a power of 8. The
rightmost position represents 8^0
(which is 1), the next position to
the left represents 8^1 (which is 8),
then 8^2 (which is 64), and so on.
3. **Counting Procedure:**
- Start with the rightmost position (8^0),
and put a digit between 0 and 7.
- Move to the left, increasing the power
of 8 by 1 each time, and again, place a
digit between 0 and 7.
- Continue this pattern as you count up.
Let's count from 0 to 15 in octal:
| Decimal | Octal |
|---------|-------|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 14 | 16 |
| 15 | 17 |
Notice that when the digit in a position
reaches 7, it becomes 0 again, and you
carry over to the next position to the
left, just like in other place value
systems. Counting in octal is a way
to represent numbers using a base-8
system, which can be useful in some
computing and mathematical contexts.
*********
*********
Due Date: August 25, 2023
Count in Hexadecimal - PX_lastname_count_Hex
Count in Hexadecimal on either the Board or
on Paper per Mr. Cusack instructions.
Take a picture with your name and class period on it.
Your file name will be PX_lastname_count_Hex.jpg
Turn it into google classroom.
Counting in hexadecimal involves
using a base-16 numbering system,
which means that each digit can
have one of sixteen possible
values: 0, 1, 2, 3, 4, 5, 6, 7,
8, 9, A, B, C, D, E, and F. Hexadecimal
is commonly used in computer science
and programming as a more compact
way to represent binary data.
Here's how to count in hexadecimal:
1. **Hexadecimal Digits:**
- Hexadecimal uses the digits
0 through 9 for values 0 to 9,
and letters A through F for
values 10 to 15.
- A corresponds to 10, B to
11, C to 12, D to 13, E to 14,
and F to 15.
2. **Hexadecimal Place Value System:**
- Similar to other numbering
systems, hexadecimal employs
a place value system.
- Each position from right to
left represents a power of 16.
The rightmost position represents
16^0 (which is 1), the next
position to the left represents
16^1 (which is 16), then 16^2
(which is 256), and so on.
3. **Counting Procedure:**
- Start with the rightmost
position (16^0), and put a
digit between 0 and F.
- Move to the left, increasing
the power of 16 by 1 each time,
and again, place a digit between 0 and F.
- Continue this pattern as you count up.
Let's count from 0 to 15 in hexadecimal:
| Decimal | Hexadecimal |
|---------|-------------|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
When a digit reaches F, it becomes
0 again, and you carry over to the
next position to the left, similar
to other place value systems.
Counting in hexadecimal provides
a convenient way to represent
binary data, as each hexadecimal
digit corresponds to exactly four
binary digits (bits), making it
easier to work with and visualize
in programming and computer-related tasks.
Converting a number from base
10 (decimal) to base 16 (hexadecimal)
involves dividing the decimal
number repeatedly by 16 and
noting the remainders at each
step. The remainders will form
the hexadecimal digits of the
new representation. Here's a
step-by-step process for converting
from decimal to hexadecimal:
1. **Divide and Record Remainders:**
- Divide the decimal number by 16.
- Note the remainder from the division.
This remainder will be one of the
hexadecimal digits (0-9 or A-F).
- The quotient obtained from the
division becomes the new value of
2. **Repeat Division:**
- Repeat the division and remainder
process using the new value of
obtained from the previous step.
- Continue this process until the
quotient becomes 0.
3. **Digits in Reverse Order:**
- Write down the remainders obtained
from each division in reverse order.
These remainders will form the
hexadecimal representation.
*********
*********
Due Date: August 25, 2023
java primitive data types "byte" size - PX_lastname_byte.png
-You will list all 8 of the java primitive data types
-indicate which are a part of the APCS A subset.
-Explain why 127 is the largest number
-allowed in the java data type "byte".
-Also, explain why I am able to store -128
-into the java data type "byte".
Take a picture of your work of the board showing your work.
Your file name will be PX_Lastname_byte.png
Turn it into google classroom.
Read the notes below:
Java eight primitive data types are:
byte 8 bits
short 16 bits
int 32 bits
long 64 bits
float 1/2 the size of double (decimal format)
double 2 times the size of float (decimal format)
boolean true/false
char single character
Why is java data type byte only stores up to 127 positive and 128 negative.
In Java, the `byte` type is an 8-bit data type that can store integer values in the range of -128 to 127. The reason for this range is due to the way binary representation and two's complement arithmetic work.
In two's complement representation, which is commonly used to represent signed integers in computers, the most significant bit (MSB), which is the leftmost bit, is used as the sign bit. If the sign bit is 0, the number is positive, and if it's 1, the number is negative. The remaining bits represent the magnitude of the number.
For an 8-bit two's complement representation, the range of values is from -2^7 (-128) to 2^7 - 1 (127). This is because the MSB represents the sign, and the remaining 7 bits represent the magnitude of the number.
Here's how it works:
- Binary representation of -128: 10000000
- Binary representation of -1: 11111111
- Binary representation of 0: 00000000
- Binary representation of 127: 01111111
As you can see, the leftmost bit (MSB) in these binary representations determines the sign of the number. If it's 0, the number is positive, and if it's 1, the number is negative. The `byte` type in Java follows this two's complement representation, allowing it to represent integers in the range of -128 to 127. This range is often sufficient for many use cases involving small integers, while also optimizing memory usage by using only 8 bits per value.
*********
*********
*********
*********
*********
*********
*********
*********